Stefan Siegert

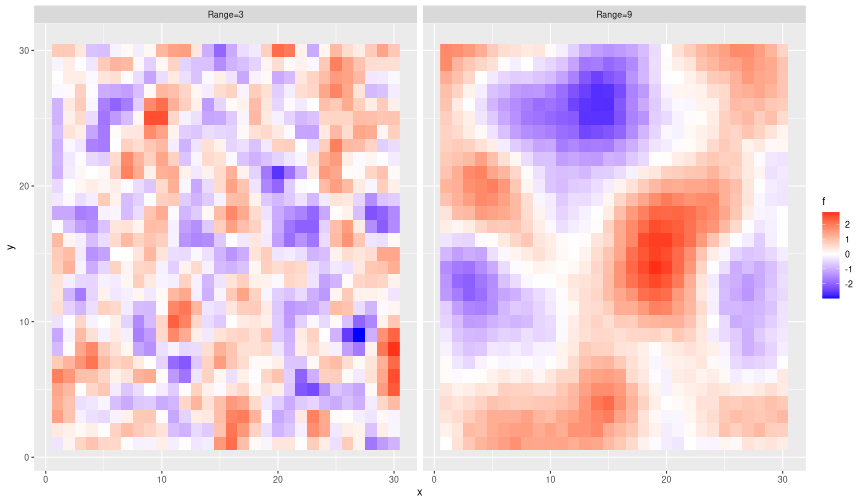
set.seed(123)
n = 30

# define grid coordinates
xy_grid = crossing(x=1:n, y=1:n)

# use `dist` to calculate matrix of euclidean distances
d = as.matrix(dist(xy_grid))

# exponential covariance function
k = function(range=1, sill=1, nugget=0.01) {
  return(sill * exp(-3*(d/range)^2) + diag(nugget, nrow(d)))
}

# draw two realisations with different range parameters
gp_sim = xy_grid %>%
  mutate(`Range=3` = drop(rmvnorm(n=1, sigma=k(range=3))),
         `Range=9` = drop(rmvnorm(n=1, sigma=k(range=9)))) %>%
  pivot_longer(c(-x,-y), names_to='range', values_to='f')

# visualise them on a grid
ggplot(gp_sim) +
  geom_raster(aes(x=x, y=y, fill=f)) +
  facet_wrap(~range) +
  scale_fill_gradient2(low='blue', high='red')
Stefan Siegert

Sampling a 2d Gaussian process
