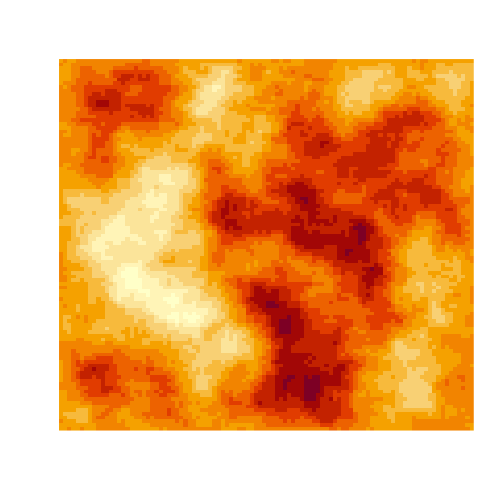
Sampling the 2d random walk
The RW2D is a 2-dimensional random field \(u_{i,j}\) characterised by the intrinsic auto-regression
\[u_{i,j} = \frac14 (u_{i-1,j} + u_{i+1,j} + u_{i,j-1} + u_{i,j+1}) + \epsilon_{i,j}\]
where \(\epsilon_{i,j} \sim N(0,\tau^{-1})\) is independent Gaussian noise with precision \(\tau\). The RW2D is widely used as a spatial prior in Bayesian hierarchical modelling.
Sampling realisations of the RW2D is not completely straightforward, since \(u_{i,j}\) depends on its neighbors, which in turn also depend on their neighbors. There is no natural starting point. Time series models like AR(1) or the random walk have a well-specified "forward direction" which makes sampling straightforward. Sampling the RW2D on the other hand needs a bit more work.
Let the \(n \times n\) matrix \(U\) denote a realisation of the RW2D random field. Define the tri-diagonal \(n \times n\) matrix \(D\) as
\[D = \frac14 \begin{pmatrix} 2 & -1 & \\ -1 & \ddots & \ddots \\ & \ddots \end{pmatrix}.\]
Then the matrix \(E\) defined by \[E = DU + UD \] is a \(n \times n\) matrix of iid Normal random variables with mean zero and precision \(\tau\).
This is a Sylvester equation so it can be rewritten in vectorised form as
\[vec(E) = (1_n \otimes D + D \otimes 1_n) vec(U)\]
where \(1_n\) is the \(n\)-dimensional identity matrix, \(\otimes\) is the Kronecker product, and the vectorisation operator \(vec(\cdot)\) transforms a matrix into a vector by column-stacking.
The vectorised equation suggests a way to simulate an RW2D random field \(U\) by first generating a vector \(e\) of \(n^2\) iid Normal variates, and multiplying it by the inverse of the 2d differencing matrix, i.e.
\[u = (1_n \otimes D + D \otimes 1_n)^{-1} e.\]
Recasting the \(n^2\) vector \(u\) back into a \(n \times n\) matrix \(U\) yields a realisation of an RW2D.
In R, this is done as follows:
library(Matrix)
set.seed(123)
n = 100
In = Diagonal(n)
Dn = 0.25 * bandSparse(n=n, k=0:1, symmetric=TRUE,
diagonals=list(rep(2, n), rep(-1, n-1)))
DD = kronecker(In, Dn) + kronecker(Dn, In)
uu = solve(DD, rnorm(n^2))
U = matrix(uu, n, n)
image(U, axes=FALSE)