This note goes over a simple agent based model of infectious disease spread written in base R. It's part of a collection of simulation models that I'm using as part of a course on Uncertainty Quantification.
Also, yes, I do realise I'm about 5 years late to write about agent-based modelling for disease spread, but whatever.
I was first looking at ABM frameworks such as NetLogo and Mesa, but kept running into small but annoying installation issues. I also realised that the minimal model I wanted to code up doesn't really need an external library at all, and could write it quite quickly in base R and maybe learn something in the process.
Here is the actual model: A number of agents move around independently and randomly on a bounded domain. Initially one agent is infected with a disease, and all others are healthy, but susceptible to being infected. Whenever a susceptible agent gets close to the infected one, it also becomes infected with some probability. Once an agent becomes infected, it can pass the disease on to other susceptible agents that it meets. After an agent has been infected for some specified time, it recovers. It is now not infectious anymore, and also cannot become infected again. The parameters of this model are the number of agents, their speed of movement, the radius of infection, the probability of infection, and the recovery time.
The full R script for this simple model can be downloaded here: sir.R. The actual code is only about 50 lines, and no external libraries are required. The code is described in detail below. Here is a visualisation of the final result, where blue is susceptible, red is infected, and green is recovered.
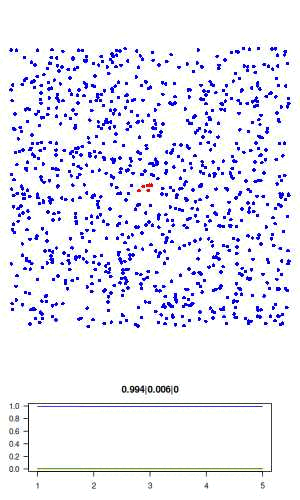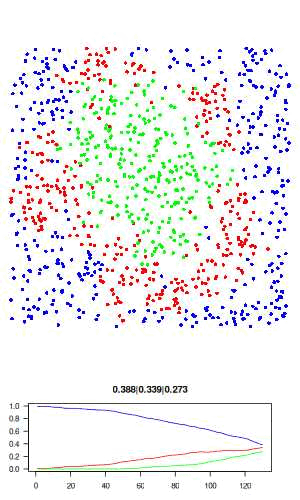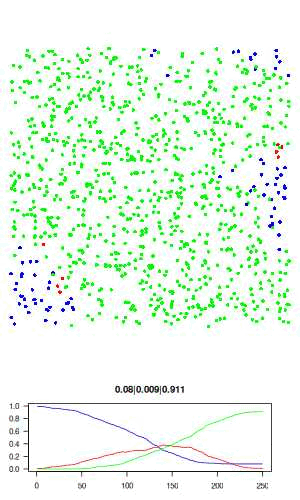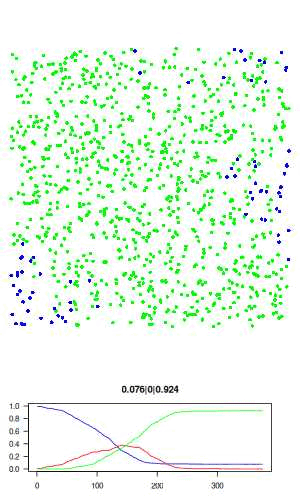
Now let's go over the R code. We first assign all model parameters within an empty list called "agents"
# initiliase list of model parameters agents = within(list(), { n_agents = 1000 # number of agents p_inf = 0.5 # probability of infection on contact r_inf = 0.02 # radius that defines "contact", as fraction of domain width t_rec = 20 # time to recovery w_step = 0.02 # maximum step width in each direction, as fraction of domain width })
Using "within(list(), {...})" instead of just "list(...)" isn't really necessary. But it makes explicit that we're using the "agents" list as an environment within which the simulated agents' state will be stored and manipulated.
Within the "agents" object we initialise random x and y locations for all agents in a Nx2 matrix. The agents' current states are stored in a vector of length N, where 0 indicates susceptible, 1 indicates infected, and 2 indicates recovered. Infection times are stored in a separate vector of length N, initially as NA for all susceptible agents. Upon infection, the agent's time is set to the recovery time (it will be decreased by one on each simulation step). We also initialise a history object in which we later store the fraction of susceptible, infected and recovered agents at each time step.
# initialise state variables (agent coordinates, infection state, infection # time). initially, just one agent at the center is infected. agents = within(agents, { # initial locations are uniformly distributed xy = cbind(runif(n_agents), runif(n_agents)) # at first, all are susceptible (state = 0) state = rep(0, n_agents) time = rep(NA, n_agents) # i=1 is patient zero located at center xy[1, ] = c(0.5, 0.5) state[1] = 1 time[1] = t_rec # initialise history object history = matrix(nrow=0, ncol=3) })
Now for the updating function which evolves the agents forward in time. It will be used by calling "agents = update(agents)" iteratively. In each update step, agents first move by adding small random numbers to their x and y coordinates. Next, to determine which agents are in contact, we calculate all pairwise distances between agents, and look for pairs whose distance is below the infection radius. If an agent is currently infected (state=1) then all of its neighbors that are susceptible (have state=0) randomly change their state from 0 to 1 with the given infection probability. Next, recovery times of all infected agents are decreased by one. Agents whose recovery time has reached zero get their state set to 2 for recovered. Newly infected agents get their recovery time initialised. Lastly, we append the current fraction of susceptible, infected, and recovered to the history object.
# agent updating function (move, infect, recover) update = function(agents) within(agents, { # # move agents randomly, ensure they don't leave the domain rand_step = matrix(runif(2*n_agents, -w_step, w_step), ncol=2) xy = pmax(pmin(xy + rand_step, 1), 0) # # calculate all pairwise distances and identify neighbors distmat = as.matrix(dist(xy)) diag(distmat) = Inf # to exclude self from neighbors neighbors = which(distmat <= r_inf, arr.ind = TRUE) # randomly infect susceptible neighbors for (ii in seq_len(nrow(neighbors))) { i_from = neighbors[ii, 1] i_to = neighbors[ii, 2] if (state[i_from] == 1 & state[i_to] == 0) { state[i_to] = ifelse(runif(1) < p_inf, 1, 0) } } # # decrement recovery time of infected, initialise recovery time of newly # infected, and recover agents where recovery time is zero time = pmax(time - 1, 0) time[ is.na(time) & state == 1 ] = t_rec state[ time == 0 ] = 2 # update history new_row = c(s=mean(state==0), i=mean(state==1), r=mean(state==2)) history = rbind(history, new_row, deparse.level=0) })
Visualisation is optional, but fun. The visualise function produces a plot of agents positions, with their state color coded. It produces a second plot underneath showing the entire history.
# visualisation function: scatter plot of agents and time series of SIR # history. use dev.hold and dev.flush to avoid flickering plots. visualise = function(agents) with(agents, { dev.hold() layout(c(rep(1,3), 2)) # plot agents par(mar=c(0,0,0,0)) plot(xy, col=c('blue','red','green')[state+1], pch = 16, ann=FALSE, axes=FALSE, asp=1, xlim=c(0,1), ylim=c(0,1)) # plot history par(mar=c(3,3,3,3)) matplot(history, type='l', las=1, col=c('blue','red','green'), lty=1, ylim=c(0,1), main = paste(tail(history, 1), collapse='|')) dev.flush() })
With the "agents" object intialised and the "update" and "visualise" functions defined, we can now iteratively update the agents' state inside a loop, and visualise their state at each step. We monitor the history and stop the simulation when nothing changes over a number of steps.
# main loop: simulate, visualise, check for stopping condition while(1) { agents = update(agents) visualise(agents) # stop if state doesn't vary for 50 timesteps past = tail(agents$history, 50) var_past = apply(past, 2, var) if (nrow(past) == 50 && all(var_past == 0)) { break } }
Apart from being coded in base R, the main bottleneck of the code is currently that I calculate distances between all pairs of agents to determine neighborhood. To make the simulation more efficient, I could, for example, calculate only distances for infected agents. But that's for another day.